
































































LES NOMBRES ENTIERS : Dans tout leurs développements des multiples

Les premières pages en cours « a g e n p h », nous ont fait découvrir le système hexadécimal qui nous délivrait son propre code décimal.
Rappel : La dernière suite était (1/6, 2/6, 3/6, 4/6, 5/6, 6/6). Puis, il y a eu (7/6) qui a pour quotient 1,166666666666670. Sept sixième comporte les mêmes décimales que (1/6), qui donne 0,166666666666667. Seule l’unité entière a progressé d’un rang, zéro virgule est devenu un virgule.
|
Or, nous savons que la première colonne contient des nombres impairs pouvant être premiers. Il y a un moyen de découvrir sa primeur, autrement qu’en cherchant au travers les multiples inférieurs…… |
Commençons par réaliser quelles sont les relations des multiples parmi les décimales!
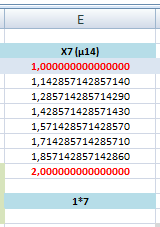
Avant de développer les décimales des multiples, nous allons comprendre comment parvenir à créer cette évolution. Comme en musique, on commence par la tonique naturelle, on commence par 1. La division qui a pour quotient 1, en ayant pour diviseur 7, c’est le chiffre sept (lui-même). En effet 7/7=1. Chronologiquement, pour aller à deux, il faut compter jusqu’à 14 parce que 14/7=2. Ce qu’il y a entre 1 et 2, se trouve être cette suite :
7/7, 8/7, 9/7, 10/7, 11/7, 12/7, 13/7, 14/7…. Nous voyons très bien les quotients ci-dessus, sur la table …(µ14).
|
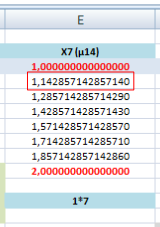
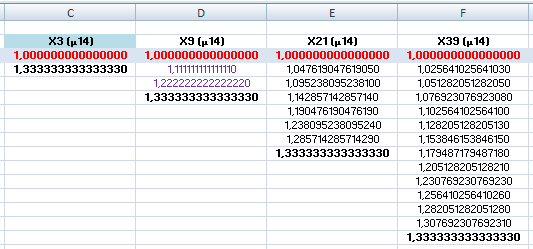
La communauté des multiples Le premier multiple de 7 c’est 14, qui est aussi un multiple de 2. Alors on se demande, quels sont les décimales communes à ces multiples ? - C’est ce qu’on peut voir… Les multiples n’ont pas de secret pour les décimales, ils arrivent toujours à détecter leurs présences. Pour ceci, il faut les avoir gardées en mémoire thématique. Tout dépend de la précision du calculateur, tellement il est vrai qu’à la main ce travail est fastidieux. |














|
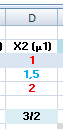
Le nombre 3 se démultiplie en commençant par lui-même, il cautionne ainsi sa première particule multiple.
La démultiplication de la division d’un même nombre, est quotient 1.
Et, incrémenter le dividende de 1. Désigne le multiple relatif 3 en position du diviseur commun. Dès lors, que le dividende a été incrémenté de 1. Nous sommes passés à la phase décimale du multiple significatif, qui a pour quotient le premier multiple commun que nous retrouvons dans les rangées supérieures des subdivisions des nombres entiers multiples de 3, pour le cas. |
* * * Le nombre de subdivisions engendrées par la démultiplication du nombre entier 3, est inférieur à celui de la démultiplication du nombre 9.
L’évolution des intervalles est constant, il suit un ordre de grandeur régulier. Ainsi, pour aller de 1 à 2. Il faut parcourir plus de divisions à chaque fois, en sachant que : 9/9=1. Et, 18/9=2. * * * |
|
Aussi, la première division qui calcule le pas de la subdivision d’un entier commun. A une valeur fondamentale, qui se retrouve parmi tous ses multiples entiers. Cette étape d’intervalle est importante, tant on sait le nombre de nombres entiers à évaluer. Dans le flux des multiples, plus on remonte le courant, et moins on traverse de subdivisions. La subdivision produit de l’intervalle. |