



































































Le numéro de l’entière histoire…
Comme référence, les premiers nombres entiers productifs en multiples communs, et rassemblant les tempéraments aux types originaux.
Puisqu’une infinité de nombres entiers vient se rassembler autour d’un unique système…
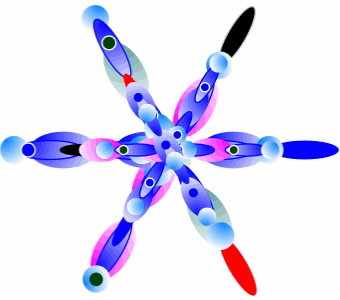
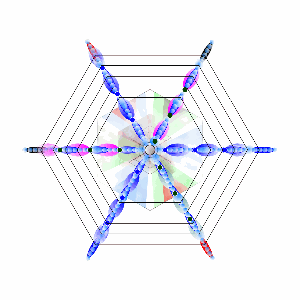
Puisse-t’on à partir d’un simple hexagone développer plusieurs tempérants ?
Pour comprendre la complexité de sa forme, il faut savoir que seulement six tempéraments dessinent cette étoile. Au cas par cas, chaque tempérament a sa propre quantification numérique. Aussi, que ce cas puisse être modifiable. Alors il suffit de le déplacer objectivement, selon l’organisation de l’unité complexe. Chacun des six premiers d’entiers sont autant de tempéraments, évoluant tous d’une même cadence. Un rythme numérique qui est une tranche de six chiffres consécutifs, ayant pour origine un nombre premier d’entier.
Le sens harmonique du nombre n’est pas identique à celui de l’harmonie musicale, c’est différent :
- Les nombres entiers sont décimaux, ils développent un modèle hexanumérique.
- Les notes musicales définissent une quantification personnelle de l’unité.
Pour définir l’harmonie des nombres entiers, réunissant le flux d’un système décimal au rythme hexanumérique. Une sorte de gamme numérique dessinée par le tempérament d’entier.



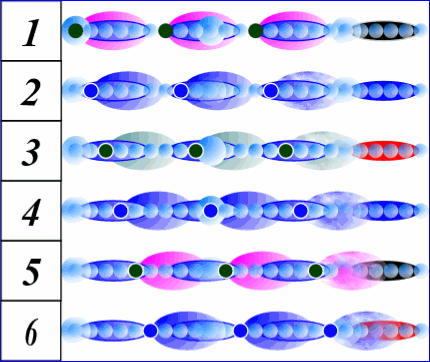


LES NOMBRES ENTIERS : Classement des premières évolutions….

|
Ces six premiers nombres forment les tempéraments initiaux… . Selon les deux triangulaires couplées, elles dessinent ainsi les rayons porteurs des nombres à l’infini. Le nombre et ses qualités :
|
|
Ce système est intéressant, car il procède à répertorier les nombres sous cette série de types :
|


Puis, un petit manuel de référence. Il décrit le comportement des nombres entiers, les formations des multiples et leur codification quantum numérique. Tout un univers d’explications réunies, pour réaliser la définition du domaine hexanumérique. |



|
# Définition exacte des nombres entiers # Dans le système hexanumérique for n in range(1,1000): if (n <= 6) : tour = 0 else : tour = 1 x = n%6 # Module d'analyse if (x == 1) : if (tour == 0) : print (n, 'premier multiple') else : print (n, 'possible premier') if (x == 2) : if (tour == 0) : print (n, 'premier multiple') else : print (n, 'multiple de 2') if (x == 3) : if (tour == 0) : print (n, 'premier multiple') else : print (n, 'multiple de 3 impair')
if (x == 4) : print (n, 'multiple de 2')
if (x == 5) : if (tour == 0) : print (n, 'premier multiple') else : print (n, 'possible premier')
if (x == 0) : print (n, 'multiple de 3 pair') |