




































































LES NOMBRES ENTIERS : L’élémentaire complexe….

Le temps imparti aux grands nombres se veut colossal, lors de la lecture séquentielle. Une seul lecteur pour un si grand nombre, voilà une bonne raison pour ajouter des lecteurs supplémentaires.
Le lecteur itératif a un point de départ, qui se situe à un endroit bien particulier. Restant à déterminer selon les différentes tournures produites par les ensembles communs.
La racine carrée du nombre donne une valeur précise, tout en limitant l’espace de lecture. L’élément premier universel numéral (1) finalise la séquence en terme premier.
Ensuite, faire un éventail sur les lecteurs…


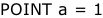


Les points (a, b, c, d) sont des nombres calculés, et ils ne sont pas obligatoirement des communs. Ils ont l’avantage d’être placés à distance paramétrée, ce qui pour les nombres à une moyenne quantité de chiffres est un bon départ.
L’exemple donné du « POINT d » fait référence au nombre entier (625) :
- Il forme la réunion de ces multiples communs couplés : 1*625 | 5*125 | 25*25
Qui a comme communs ces nombres (1, 5, 25, 125, 625). Plus faciles à trouver avec une application, de cette série est composée des nombres par lesquels peuvent s’opérer les divisions entre nombres entiers produisant des quotients entiers. Ex… 625/25 = 25.
Les points des lectures simultanées dans l’espace carré de la racine du nombre donné, ici (625). Se retrouvent dans une situation de gestion appliquée, au sujet de la manière de chercher qui change d’un type à l’autre. Comme son nom l’indique, le nombre premier a de grandes chances pour qu’une toute autre lecture que le nombre (1) ne soit vaine. Ce qui implique une utilisation évoluée des points de lecture, ce qui est un autre sujet. Autrement, les nombres originaux de type (2, 3, 4, 0) ont la propriété de composer des communs entiers non premiers.
Les types de bases paires (2, 4, 0(6)), et impaires (1, 3, 5), s’organisent en une parité de deux et une imparité de trois. La typologie paire et impaire est activée via le tempérament, la consistance d’un nombre de type pair cadençant la chronologie des sous-multiples communs. Toute cette communauté forme un unique topo, aidant l’imaginaire à dessiner les traces laissées par les tempéraments des communs multiples exprimés en nombres entiers.
Nous l’avons tous compris, la variété des types a des intervalles parfois importants et à positions opposées. Détecter les points de lecture est une stratégie « gain de temps », et association aidant. Il est exact de dire que le sous-multiple est un nombre inférieur au multiple, et d’entendre que le sous-multiple est d’autant plus rapide à calculer. Il ne faut pas négliger le temps de lecture lors de la recherche, au détriment de celui du traitement suivant. Il y a un équilibre à réaliser entre les traitements, et autrement parler de l’équilibre culturel par l’exemple d’une démonstration. Où l’intérêt de voir un traitement porté sur une technique de lecture, simpliste et claire.
C’est intéressant de lire des histoires sur les nombres, d’autant plus à un niveau moyen (en relation avec l’auteur). Les groupes multiples connaissent des éléments préalables premiers, voire même premiers. Les nombres premiers au milieu des communs classiques, voilà un sujet de converse. Qui va bien avec une lecture ne trouvant que les nombres aux préalables premiers, ceux-mêmes qui font les tempéraments concentrés. Oui, puisque multipliés par eux-mêmes, ils résolvent l’équation. Cette technique est une bonne approche…
Dans un passé récent, un groupement de type zéro (6). Ce genre de typage a de nombreux couplages communs, ainsi que l’occurrence d’un nombre premier en terme de l’élément du couple supérieur au niveau du carré. Un couple commun est formé par deux nombres, qui lorsqu’ils sont multipliés, produisent le nombre initial du groupe. Le couple de haut niveau pour le nombre initial (625), est 1 * 625. Le couple de bas niveau, qu’il soit proche ou égal à la racine, est 25 * 25. Ici, il s’agit bien d’un carré à la racine. Ils ont tous deux les mêmes multiples communs…
Un cas exceptionnel, tant que l’élément inférieur du couple de bas niveau, qui lorsqu’il est accompagné d’un entier réellement premier. Détient dans sa composition tous les éléments inférieurs des couplages, c’est dire qu’il a le pouvoir de résoudre cette équation…
- Pour un groupe initié au nombre (625)
« I P » = 1 * « D V » = 625. Couple niveau haut
« I P » = 5 * « D V » = 125. Couple niveau…
« I P » = 25 * « D V » = 25. Couple niveau bas
En fait, tout est d’exception. Ce qui nous informe sur des valeurs formelles, et plus exactement sur les comportements des multiples. D’une complexe variétés et toujours à découvrir, elle est l’ensemble des points de repères que doivent obtenir les lectures itératives.
La composition des communs du nombre original (625), est une suite de préalables premiers. En transposant ses éléments à l’aide d’un mode opératoire différent, on a une série de repères calculés. Petit rappel élémentaire : {1, 5, 25, 625}. Ce qui ressemble à une répétition de racines carrées : {(5*5), (25*25)}. L’exposant {5*5 = 25} a son rapport carré {25**.5 = 5}, en en suite du petit rappel {n**.5, n**.25, n**.125}. Et par définition ; Les bases retenues.
Les échelles obtenues et leurs larges choix de composition, vont faciliter le placement des points par une opération directe et non en lecture séquentielle. Par simplicité ne sont détaillés que les quatre premiers points (a, b, c, d):
- Le point a
La lecture du nombre un (1) n’est effectuée qu’après les lectures des autre points, étant donné qu’il est commun à tous les nombres. Il n’est pas l’unique multiple commun dans de nombreux cas.
- Le point d
La lecture du nombre calculé « 625**.125 = 2.23606797749979 » (2) en partie entière, est le pas de courte distance. Qui a cause de cette faible mesure, significative aux grands nombres.
- Le point c
La lecture du nombre calculé « 625**.25 = 5.0 » (5) en partie entière, et (racine carrée)². Nombre premier du bas niveau, et multiple commun événementiel.
- Le point b
La lecture du nombre calculé « 625**.5 = 25.0 » (25) en partie entière, et unité racine carrée. Nombre du niveau intermédiaire, et multiple commun événementiel.
Telle qu’on peut le décrire, la multiplication nécessite un multiplicateur et un multiplicande, d’où le couple de multiples communs au nombre produit. Il n’est pas impossible que ce nombre produit ait d’autres multiples communs, tel le nombre (625) qui a trois couplages. Et c’est cette séquence qui nous informe sur les adaptations relatives aux racines carrées pour les lectures, et de l’exactitude de la proportion de son unité.
- Pour un groupe initié au nombre (625)
« I P » = 1 * « D V » = 625.
« I P » = 5 * « D V » = 125. « I P » 625**.25 événementiel commun
« I P » = 25 * « D V » = 25. « I P » 625**.5 événementiel carré
« I P » = 125 * « D V » = 5.
« I P » = 625 * « D V » = 1.
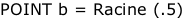

1 |
625 |
|
5 |
125 |
|
25 |
25 |
|
125 |
5 |
|
625 |
1 |