






























































LES NOMBRES ENTIERS : Le nombre entier et sa quantique élémentaire….
Les chiffres tels qu’ils se suivent, nous décrivent une harmonie numérique. Du premier chiffre « 1 » à l’infini, en passant par « 6 », parfois multiples ou premiers. L’opération des nombres pairs et impairs donne souvent des chiffres différents, alors comment comprendre cette évolution ?
Les nombres ont plusieurs particularités, ils sont pairs ou impairs, entiers ou décimaux selon qu’ils soient multipliés ou divisés. Tout comme la musique mineure, il y a les chiffres décimaux. La fraction de l’unité et sa finesse décimale, pour mieux cerner les tempéraments qui procèdent logiquement. À l’inverse de la multiplication, il y a la division logique de l’intervalle !
Petit à petit, le sujet se développera sur ces explications. Puisqu’il s’agit d’un complexe numéral, qui doit évoluer en termes clairs sans aucune vélocité d’exécution. Les nombres vont être découverts dans des situations élémentaires et harmoniques, soit en exerçant un travail d’artiste…

La composition des nombres en décomposition !
La division des nombres donne des nombres décimaux, c’est selon leurs multiples originaux que vont être interprétées les différentes natures des chiffres. En multipliant 1*2 on a le même résultat en faisant 2/1…
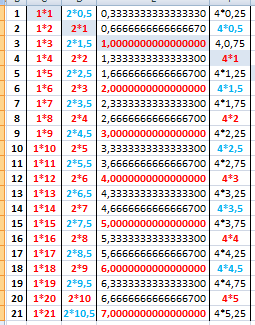
En prenant l’exemple du tableau ci-contre, qui traite des nombres de 1 à 21. Les nombres entiers donnés, forment les dividendes. Chaque diviseur est traité par la série des dividendes, ils constituent une colonne des subdivisions relatives. Toutes ces divisions colonisées en un point commun, relatent le tempérament du diviseur dans l’évolution des nombres entiers.
Le caractère décimal du chiffre « 3 » offre une série remarquable, en un premier temps de multiplicité. Ces intervalles avec virgule comportée a deux fixations (0,333… & 0,666…), qui sont à l’origine des nombres premiers. D’où une description des valeurs premières, qui ne se répètent pas sous peine de devenir des multiples secondaires….
La composition des intervalles aux cas de figures multiples.
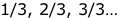

|
Dans le développement des nombres ayant une même série de dividendes, il y a une extrapolation qui passe par les multiples communs. Ainsi, chaque degré des chiffres, a des familiarités répandues parmi les subdivisions. Donc, la subdivision complète harmoniquement la multiplication. Elle est le sens caché de l’expression des nombres entiers. Ainsi, l’intervalle est un moyen de comparer les nombres entiers en définissant s’ils sont premiers. Pour l’instant, nous prenons juste connaissance de la logique formée par un même dividende. |


|
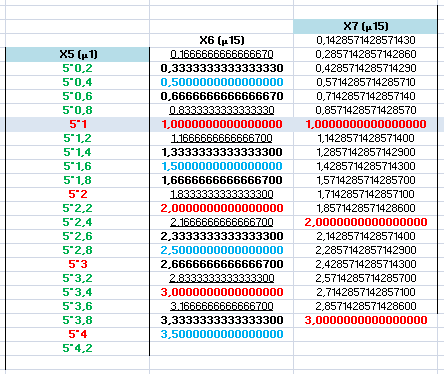
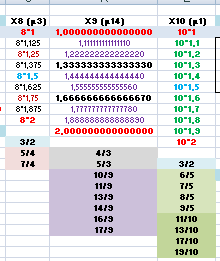
Précédemment, les épisodes des dividendes concernaient les nombres entiers de 1 à 21. Et hiérarchiquement, les formes s’incrémentaient d’une unité. Entre 1 & 2, il y a tout le nécessaire pour une bonne analyse. Puis, ce qu’il y a entre 3 & 4 est pratiquement identique, sauf pour l’unité entière du nombre décimal. Aussi, le tableau de gauche, développe les intervalles relatifs aux nombres. Décrit les correspondances depuis la source commençant à un, à chaque fois. Le monde des fractions s’organise en une chronologie qui n’est pas aléatoire, puisqu’au fur et à mesure elles développent des multiples. Il y a de nombreuses connections multiples, et ce qui peut paraître compliqué actuellement serait mis en lumière avec d’autres compositions. Car, il y avait l’élément multiple. Qui était subdivisé en découvrant des régions, à l’aide des dividendes révélateurs. Ainsi, que tous les nombres multiples de 3 ont les mêmes indices décimaux. Idem pour les autres catégories de chiffres…. |
1,333333333333330 : expression de 4/3, 8/6, 12/9, 16/12, 20/15, 24/18, 28/21…
1,666666666666670 : expression de 5/3, 10/6, 15/9, 20/12, 25/15, 30/18, 35/21, 40/24…
1,1111111111111100 : expression de 10/9, 20/18, 30/27, 40/36, 50/45, 60/54…