


































































Épisodes passés & anciens présents
Multiples communs primaires
Épisode des comparaisons
for iep in range(sq5, i0, -1):
if not uz % iep \
and iep % 6 in (1, 5):
Un nombre est incrémenté pour être comparé, le motif de comparaison est pour le cas le reste de la division. Ainsi pour un nombre « uz » comme unique argument de la recherche des communs, a un nombre incrémenté auquel il opère « if not uz % iep ». Si « uz % iep » égale zéro, c’est qu’il s’agit d’un sous-multiple. Étant donné que la recherche s’effectue sur les préalables premiers, autant ajouter à la condition « if », ceci « and iep % 6 in (1, 5) ». Cette opération produit le reste comme précédemment, avec diviseur le six filtrant le type correspondant aux valeurs un ou cinq. Cette comparaison { Nombre % Multiple | Multiple % 6 } revient souvent, comme on peut le voir sur le code…
Identification des communs
Épisode des affectations
Sont affectés les compteurs, les types, puis les nombres ont des ressources affectives. En sachant que les préalables ont des types alignés (1&5), et que le basique incrémenté est six. Ainsi, en ajoutant six à chaque pied de lignée, en bref : On suit la lignée. L’épisode des comparaisons relate les types préalables, et des motivations de cet exercice assigné sur un nombre incrémenté. Les grands nombres ont des grands intervalles limités par les communs (voisins dirait le tempérament), et comme il n’y a pas encore de recette miracle. On crée des compteurs sur lesquels vont être effectuées les itérations, aussi. Les compteurs sont liés à la racine carrée du nombre sur lequel se porte cet exercice, ils sont répartis en trois tableaux. Et chacun d’entre eux comporte trois éléments, disons que le tableau racine soit s_01 :
Alors, s_01 [0] = Type original,
et, s_01 [1] = Nombre type 1,
puis, s_01 [2] = Nombre type 5.
Étant donné qu’il y a deux lignes contenant les préalables premiers, et qu’elles sont incrémentées de six. Et qu’en différant de l’incrément un, et en faisant un pas plus grand. Et puisqu’à l’origine les compteurs sont présents, a mis à part de l’incrément, ils ont étés couplés aux données des tableaux. Donc, pour ce qui était une poursuite horizontale, du genre l’itération de un à douze sur le chemin couché des nombres.
Certes ça passe par (1, 2, 3, 4, 5, 6, 7, 8, …, 11, 12), selon la matrice qui superpose les couches aux six nombres consécutifs. En réalisant une poursuite verticale là où le pas est augmenté, lorsque les deux types ont un unique point commun à chacune des couches développées.
Temporisation communale
Épisode des temporisations
La série des nombres en couchettes et leurs rêves alignés, et le rapport d’intervalle 6 qui en découle. Les alignements des types non significatifs, soient à terme élémentaires en décrivant ce même intervalle. En connaissant la notion des nombres premiers, celle qui dit :
Dans le cas d’une grande quantité de sous-multiples à un nombre unique.
À eux seuls, les nombres premiers (sous-multiples) produisent tous les communs.
Dans un premier temps, les compteurs organisent la répartition des lectures. Qui sont placées selon les racines carrées, et ainsi avoir des positions calculées à l’aide d’un espace donné. Le principe simple de lecture des nombres premiers, consiste à vérifier l’existence d’un sous-multiple de ce nombre situé dans une des lignées relative aux nombres préalablement premiers. Pour y parvenir il faut définir un groupe de nombres premiers basiques, qui met en relation les nombres premiers n’étant pas dans les lignées (1&5).
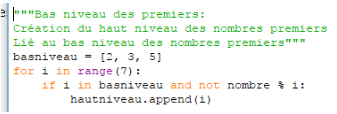
Les nombres primaires premiers sont (1, 2, 3, 5) : Bas niveau = [2, 3, 5]. Le nombre 1 est un multiple commun universel, il n’est pas dans le groupe premier puisqu’il empêche la vérification des autres opportunités en déclarant la présence d’un sous-multiple. Le nombre 5 est présent puisque l’ordonnance a un tempérament de six, permettant la bonne régularité de son cours.
Quant alors, ces définitions visant à exprimer un cours sur les tempéraments et de leurs compositions familières aux multiples. Puis de cette requête des diviseurs entiers, en nombres premiers sélectionnés comme premiers communs. Ces derniers premiers diviseurs, et leurs multiplications forment des stratifications communes à un unique nombre original mais pas isolé. Selon, la recherche des communs de deux nombres originaux non divisibles entre eux et, qu’ils ne soient pas d’ordre premier. Chaque nombre a une liste premiers communs, rassembler ces deux listes consiste à multiplier les deux nombres originaux.



LES NOMBRES ENTIERS : Temporels premiers.



Épisodes passés & anciens présents
Passifs :
- Multiples communs primaires
Épisode des comparaisons - Identification des communs
Épisode des affectations - Temporisation communale
Épisode des temporisations
Le niveau bas des nombres premiers Définition hors lignes (1&5), en base 6. |
|
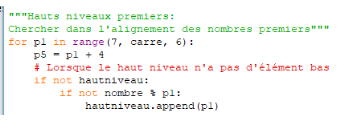
Le haut niveau initial du groupe Lorsque le groupement du démarrage est vide, la comparaison n'est pas possible. Si ce cours ne trouve pas une solution à terme, c'est qu'il n'y en a pas. |
|
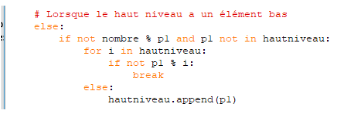
Le haut niveau final du groupe Les nombres préalablement premiers, ne sont pas tous premiers. Et souvent, le groupe ne sera pas vide. Haut niveau = [] |