


































































- Pour un groupe initié au nombre (625)
« I P » = 1 * « D V » = 625. Couple niveau haut
« I P » = 5 * « D V » = 125. Couple niveau…
« I P » = 25 * « D V » = 25. Couple niveau bas
Ces « I P » multipliés à leurs « D V » respectifs, produisent les mêmes résultats…
Ainsi, six cent vingt cinq a quatre unités : 1, 5, 25, 125. Ils sont tous de type (1 ou 5), soit préalables nombres premiers. Mais, ce n’est pas une prédilection. Puisqu’au final, seuls les nombres (1 & 5) sont des nombres premiers. Qui produisent un ensemble de tempéraments.
Afin de multiplier ces deux nombres premiers, on peut choisir de créer deux tableaux :
- Le tableau TIP = 1, 5
- Le tableau TOP = 1, 5
Et, de faire une lecture des éléments du tableau TOP à chaque élément du tableau TIP.
Ce qui en langage codé s’apparente à ceci :
While 1:
IP = len(TOP)
N = 625
For i in TIP:
For y in TOP:
X = i * y
If not N % X and not X > N and X not in TOP:
TOP.append(X)
OP = len(TOP)
If IP == OP:
Break
Transcription du code en langage classique.
En créant « TOP », nous savions qu’elle allait porter tous les nombres communs à « N ». Nombre original « 625 » initialisant le terme codé « N », élément de comparaison.
L’élément « i » est multiplié aux éléments « y », produisant « X » comme résultat.
Si le reste du module « X % N » est égal à zéro, alors « X » est un multiple commun.
Si « X » n’est pas supérieur à « N », ceci afin de limiter le résultat à « N ».
Si « X » n’est pas dans le tableau « TOP », alors « X » n’est pas un doublon.
Ces trois conditions « Si », sont réunies dans le but de produire un résultat exact.
While 1:
IP = Nombre d’éléments dans « TOP » (début)
For i in TIP: TIP = 1, 5
Prit 1 « i = 1 »
Prit 3 « i = 5 »
Prit 5 « i = 1 »
Prit 8 « i = 5 »
…/…
Prit 11 « i = 5 »
…/…
Prit 15 « i = 5 »
For y in TOP:
Prit 1 « i = 1 »« y = 1 »
Prit 2 « i = 1 »« y = 5 »
Prit 3 « i = 5 »« y = 1 »
Prit 4 « i = 5 »« y = 5 »
Prit 5 « i = 1 »« y = 1 »
Prit 6 « i = 1 »« y = 5 »
Prit 7 « i = 1 »« y = 25 »
Prit 8 « i = 5 »« y = 1 »
Prit 9 « i = 5 »« y = 5 »
Prit 10 « i = 5 »« y = 25 »
…/…
Prit 11 « i = 5 »« y = 1 »
Prit 12 « i = 5 »« y = 5 »
Prit 13 « i = 5 »« y = 25 »
Prit 14 « i = 5 »« y = 125 »
…/…
Prit 15 « i = 5 »« y = 1 »
Prit 16 « i = 5 »« y = 5 »
Prit 17 « i = 5 »« y = 25 »
Prit 18 « i = 5 »« y = 125 »
Prit 19 « i = 5 »« y = 625 »
X = i * y
Prit 1 « X = 1 »
Prit 2 « X = 5 »
Prit 3 « X = 5 »
Prit 4 « X = 25 »
Prit 5 « X = 1 »
Prit 6 « X = 5 »
Prit 7 « X = 25 »
Prit 8 « X = 5 »
Prit 9 « X = 25 »
Prit 10 « X = 125 »
…/…
Prit 11 « X = 5 »
Prit 12 « X = 25 »
Prit 13 « X = 125 »
Prit 14 « X = 625 »
…/…
Prit 15 « X = 5 »
Prit 16 « X = 25 »
Prit 17 « X = 125 »
Prit 18 « X = 625 »
Prit 19 « X = 3125 »
Condition « Si »:
Prit 4 « TOP = 1, 5, 25 »
Prit 10 « TOP = 1, 5, 25, 125 »
Prit 14 « TOP = 1, 5, 25, 125, 625 »
OP = Nombre d’éléments dans « TOP » (fin)
Condition « IP = OP »: Break (stop)


LES NOMBRES ENTIERS : Premiers Temps.



|
ce classeur Excel excelle L'organisation offerte par l'harmonie des nombres, dessine des lignes colorées. Cette sélection nommée a des temps linéaires et du vide, où chaque ligne oblique est un tempérament. La résolution graphique 2D indique une incohérence dans la localisation des extrémités, ou un considérable éloignement remarqué entre les nombres un et sept sur le tableau. |
|
|
tempsvide.PNG Partie d'espace ambiant, dans lequel fusent les ondes formées par les tempéraments harmoniques des nombres. En imaginant une activité visant à rétablir la justesse, non précisée dans l'incohésion parue en 2D. On en arrive au mode 3D, à décrire des spirales sur ce cours organisé. |
|



|
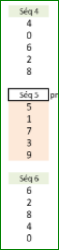
Cadences typiques et unités occultées |
|
En partant de un jusqu'à six unités, et d'à chacune unité ajouter six. Comme par exemple l'unité un à laquelle est ajoutée six, de façon itérative : 1, 7, 13, 19, 25... Cette série a pour valeurs unitaires (1, 7, 3, 9, 5), elle est répétée et alignée. Les éléments de cette répétition ont étés occultés de leurs parts décimales, ce qui n'empêche pas leur poursuite en temps réel. |